
Gyrogravity and Antigravity

This simple formula was obtained from first principles, together with the formula for G, the Gravitational Constant...:)
This is a clean and elegant derivation shown in this pdf.
Nevertheless, that was an honest overlook. Given enough time, I was able to find Gravitomagnetism entry in Wikipedia...:) which I reproduced below:
This approximate reformulation of gravitation as described by general relativity makes a "fictitious force" appear in a frame of reference different from a moving, gravitating body. By analogy with electromagnetism, this fictitious force is called the gravitomagnetic force, since it arises in the same way that a moving electric charge creates a magnetic field, the analogous "fictitious force" in special relativity. The main consequence of the gravitomagnetic force, or acceleration, is that a free-falling object near a massive rotating object will itself rotate. This prediction, often loosely referred to as a gravitomagnetic effect, is among the last basic predictions of general relativity yet to be directly tested.
Indirect validations of gravitomagnetic effects have been derived from analyses of relativistic jets. Sir Roger Penrose had proposed a frame dragging mechanism for extracting energy and momentum from rotating black holes.[1] Reva Kay Williams, University of Florida, developed a rigorous proof that validated Penrose's mechanism.[2] Her model showed the Lense-Thirring effect could account for the observed high energies and luminosities of quasars and active galactic nuclei; the collimated jets about their polar axis; and the asymmetrical jets (relative to the orbital plane).[3] All of those observed properties could be explained in terms of gravitomagnetic effects.[4] Williams’ application of Penrose’s mechanism can be applied to black holes of any size.[5] Subsequently, relativistic jets can serve as the largest and brightest form of validations for gravitomagnetism.
A group at Stanford University is currently analyzing data from the first direct test of GEM, the Gravity Probe B satellite experiment.
[edit]Equations
According to general relativity, the gravitational field produced by a rotating object (or any rotating mass-energy) can, in a particular limiting case, be described by equations that have the same form as the magnetic field in classical electromagnetism. Starting from the basic equation of general relativity, the Einstein field equation, and assuming a weak gravitational field or reasonably flat spacetime, Lano, [6] Fedosin [7] Agop, Buzea and Ciobanu, [8] Mashhoon, Gronwald, and Lichtenegger,[9] and Clark and Tucker,[10] have derived the following gravitational analogs to Maxwell's equations for electromagnetism, called the "GEM equations":
where:
- Eg is the static gravitational field (conventional gravity, also called gravitoelectric for the sake of analogy);
- Bg is the gravitomagnetic field;
- ρ is mass density (instead of electric charge density);
- vρ is the velocity of the mass flow generating the gravitomagnetic field;
- J is mass current density (J = ρ vρ);
- G is the gravitational constant;
- c is the speed of propagation of gravity (equal to, by general relativity, the speed of light).
For a test particle whose mass m is "small," the net (Lorentz) force acting on it due to a GEM field is described by the following GEM analog to the Lorentz force equation:
 .
.
where:
- m is the mass of the test particle;
- vm is the instantaneous velocity of the test particle.
In the literature, all instances of Bg in the GEM equations are multiplied by 1/2, a factor absent from Maxwell's equations. This factor vanishes if Bg in the GEM version of the Lorentz forceequation is multiplied by 2, as shown above. The factors 2 and 1/2 arise because the effective gravitomagnetic charge is twice the static gravitational (gravitoelectric) charge, a remnant of the spin-2 character of the gravitational field. For a pure spin-1 field such as the genuine electromagnetic field, the magnetic charge equals the electric charge.
For the field Bg near a rotating body from GEM equations follows:
where L is the angular momentum of the body.
[edit]Comparison with electromagnetism
The above GEM equations are very similar to Maxwell's equations in free space, which in cgs units are:
Adopting Planck units eliminates G and c from both sets of equations by normalizing these constants to 1. The two sets of equations are now identical but for the minus sign preceding 4π in the GEM equations. These two minus signs stem from an essential difference between gravity and electromagnetism: electrostatic charges of identical sign repel each other, while two like signed (positive) masses attract each other. Hence the GEM equations are simply Maxwell's equations with mass (or mass density) substituting for charge (or charge density), and -Greplacing the Coulomb force constant 1/(4πε0). The following Table summarizes the results thus far:
| Common Structure of the Maxwell and GEM Equations Given Planck units. |

ι = 1 (Maxwell) or -1 (GEM). |
The factor of 4π remains in both the GEM and Maxwell's equations because G and 1/(4πε0) are normalized to 1, and not 4πG and ε0.
[edit]Higher-order effects
Some higher-order gravitomagnetic effects can reproduce effects reminiscent of the interactions of more conventional polarized charges. For instance, if two wheels are spun on a common axis, the mutual gravitational attraction between the two wheels arguably ought to be greater if they spin in opposite directions than in the same direction. This can be expressed as an attractive or repulsive gravitomagnetic component.
Gravitomagnetic arguments also predict that a flexible or fluid toroidal mass undergoing minor axis rotation ("smoke ring" rotation) will tend to pull matter preferentially in through one throat and expel it from the other (a case of rotational frame dragging, acting through the throat). In theory, this configuration might be used for accelerating objects (through the throat) without such objects experiencing any g-forces.[11]
Consider a toroidal mass with two degrees of rotation (both major axis and minor-axis spin, both turning inside out and revolving). This represents a "special case" in which gravitomagnetic effects generate a chiral corkscrew-like gravitational field around the object. The reaction forces to dragging at the inner and outer equators would normally be expected to be equal and opposite in magnitude and direction respectively in the simpler case involving only minor-axis spin. When both rotations are applied simultaneously, these two sets of reaction forces can be said to occur at different depths in a radial Coriolis field that extends across the rotating torus, making it more difficult to establish that cancellation is complete.
Modelling this complex behaviour as a curved spacetime problem has yet to be done and is believed very difficult.
[edit]Gravitomagnetic field of Earth
- Bg, Earth = 10−14 rad·s−1[12]
See the Gravity Probe B experiment.
[edit]Fringe physics
Incomplete understanding of the meaning of the similarity of the gravitomagnetic formulas, above, and Maxwell's equations for (real) electricity and magnetism have given rise to fringe physics. Use of the gravitomagnetic analogy for a simplified form of the Einstein field equations, on the other hand, is firmly part of General Relativity. It is an approximation to the current standard theory of gravitation, and has testable predictions, which are in the final stages of being directly tested by the Gravity Probe B experiment. Despite the use of the word magnetismin gravitomagnetism, and despite the similarity of the GEM force laws to the (real) electromagnetic force law, gravitomagnetism should not be confused with any of the following:
- Claims to have constructed anti-gravity devices;
- Eugene Podkletnov's claims to have constructed gravity-shielding devices and gravitational reflection beams.
- Any proposal to produce gravitation using electrical circuits.
[edit]See also
[edit]
Despite of similar predictions, the lack of clarity of the model developed from General Relativity make it look clumsy, unelegant. It also fails to provide the dependence that would make White Orifices possible or explainable.
It fails where General Relativity should've never failed, that is, in predicting that accelerating a body towards c is more difficult than to decelerate that same object!!!!I say it fails, because it is impossible to clearly see what is happening in those Gravitomagnetism equations...:) Not to mention what possibly could justify a factor of 2 in the equations...:) (other than my Fundamental Dilator paradigm and the 4D spatial manifold, 4D Mass reformulation of Gravitational equations, etc.
Einstein said that one should make a theory (representation of reality) as simple as possible but not simpler.
I think he failed to do so, since my theory is quite simpler that his.
Much has been proposed (ad hoc) about modifications of Gravity Laws by Gerber (which matches my theory in a limit), Einstein and others. I mentioned that the velocity dependence of Gravity I found in my theory would doom Einstein paradigm of Mass-Driven Metric Deformation.
In this Wikipedia entry the authors have the same opinion:
Modelling this complex behaviour as a curved spacetime problem has yet to be done and is believed very difficult.I believe that it might be not only very difficult but also unnecessary and undesirable. Einstein equations are notoriously difficult to integrate...:) Wouldn't be great to have a potential that you can just use in Lagrangian equations and get the correct answer..:) My theory provides that potential and it is quite simple...:) The integration has to be done in the right panel of my Hypergeometrical Universe icon shown at the top of the blog, that is, in the hyperbolic spacetime, but that is a simple problem.
As you know from what I mentioned many times, I do this for fun and during my commuting to and from work...:) which leaves little time to make a decent reference review. Please, feel free to criticize or advise me about missing pieces of information.
I've never understate someone else' work to elevate mine. I believe there isn't anything in the literature that follows my line of reasoning, thus it is only gratifying to find that others (in their own way) reached similar conclusions. We are all speaking of the same reality...:)
Cheers,
MP
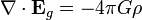
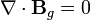

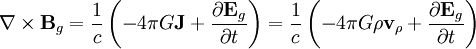

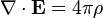
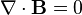
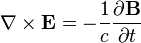




No comments:
Post a Comment